一、 概述

在控制系统算法开发中，需要对于某些重要信号做限制处理，对于限制条件恢复后，信号怎么输出的选择上也有多种选择，比如限制条件满足，对输出信号作限制，限制条件恢复，输出信号立即恢复为正常值；或者限制条件恢复，输出信号按照一定的梯度逐渐恢复至正常值等等。

具体选用哪种处理方式，取决于具体算法需求。之前的文章中详细介绍过用Simulink基本模块建模以及仿真验证的方法，本文就以上第二种信号处理方式，通过Simulink的状态流state flow来建模以及仿真验证。

二、 Simulink状态流State Flow

根据以往的汽车电控软件开发经验，以整车跛行（整车出现故障，需要进行限速）扭矩限制搭建了如下图的Simulink的状态流state flow算法模型：

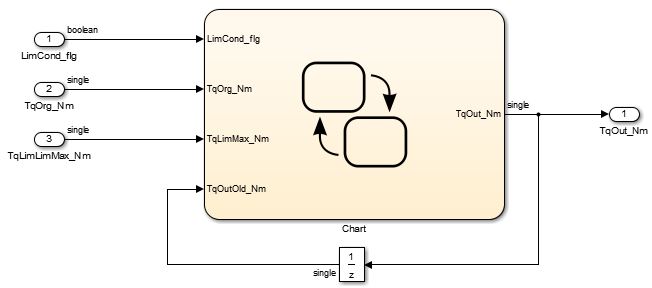
模型输入信号说明：

LimCond_flg：信号限制条件

TqOrg_Nm：原始输入扭矩

TqLimMax_Nm：限制最大扭矩

模型输出信号说明：

TqOut_Nm：输出扭矩 模型参数说明：

TqStepInc_Nm：递增扭矩

Chart由三个状态组成，具体如下：

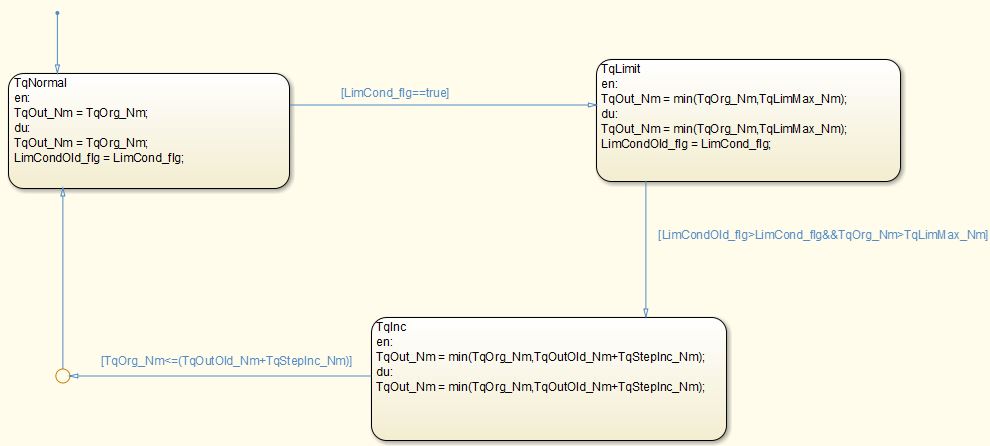
算法说明：

TqNormal状态

进入条件：上电默认状态或者TqInc状态跳出条件满足

处理：TqOut_Nm=TqOrg_Nm，并记录LimCond_flg上一次状态LimCondOld_flg=LimCond_flg

TqLimit状态

进入条件：LimCond_flg为TRUE

处理：TqOut_Nm=min（TqOrg_Nm，TqLimMax_Nm）

TqInc状态

进入条件：检测到LimCond_flg 下降沿LimCondOld_flg>LimCond_flg 且TqOrg_Nm>TqLimMax_Nm

处理：TqOut_Nm=Min（TqOrg_Nm，TqOut_Nm+TqStepInc_Nm）

跳出条件：当输出扭矩增加到大于或等于输入原始扭矩，也即：TqOrg_Nm<=(TqOutOld_Nm+TqStepInc_Nm)

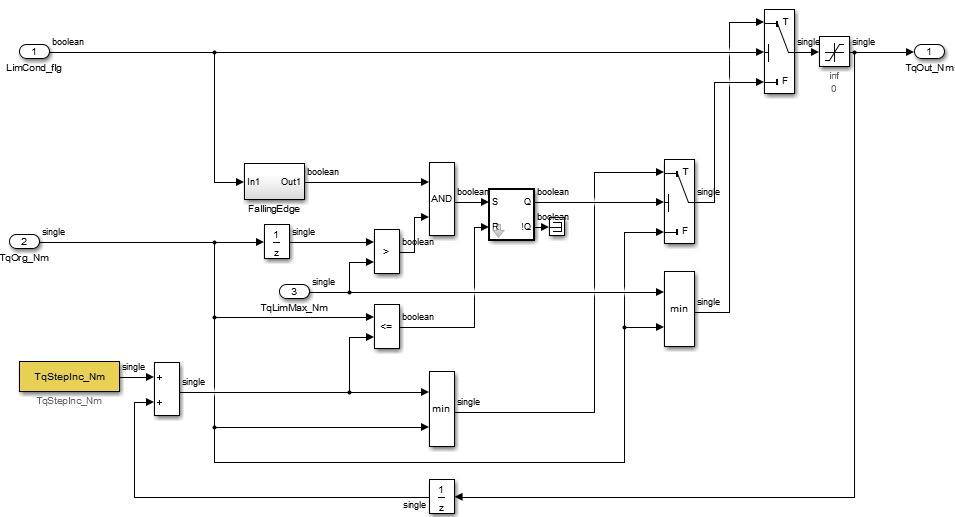
通过三个状态转移的方法，实现了原来由Simulink基本模块搭建，逻辑看起来略显复杂，且要通过S-R触发器才能锁存状态的逻辑，如下图：

三、 算法仿真验证

仿真模型：

如上的仿真模型中，给定同样的输入激励：

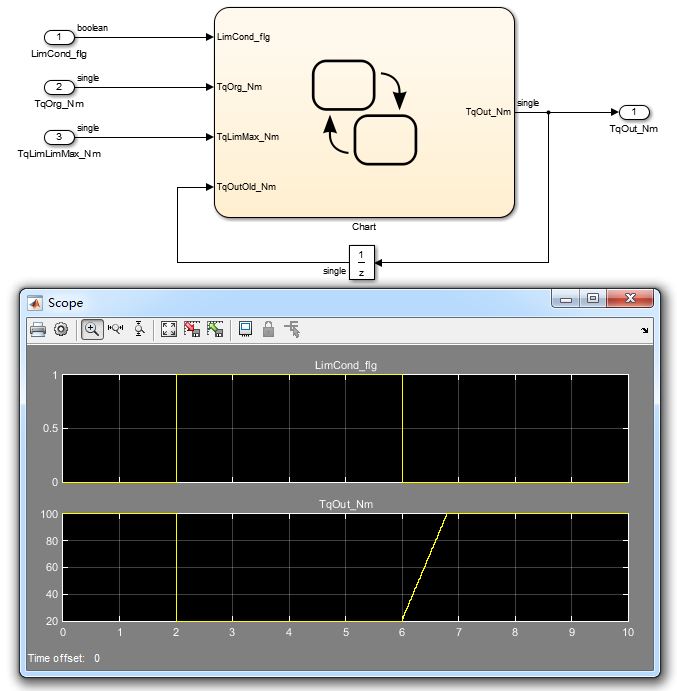
1） 通过Signal Builder模块给定LimCond_flg，0s~2s为0,2s~6s为1,6s以后为0

2） 通过Constant模块给定TqOrg_Nm为100

3） 通过Constant模块给定TqLimMax_Nm为20

4） 给定TqStepInc_Nm为1

5） 设置离散求解器，仿真步长为0.01s，仿真时长为10s

仿真结果：

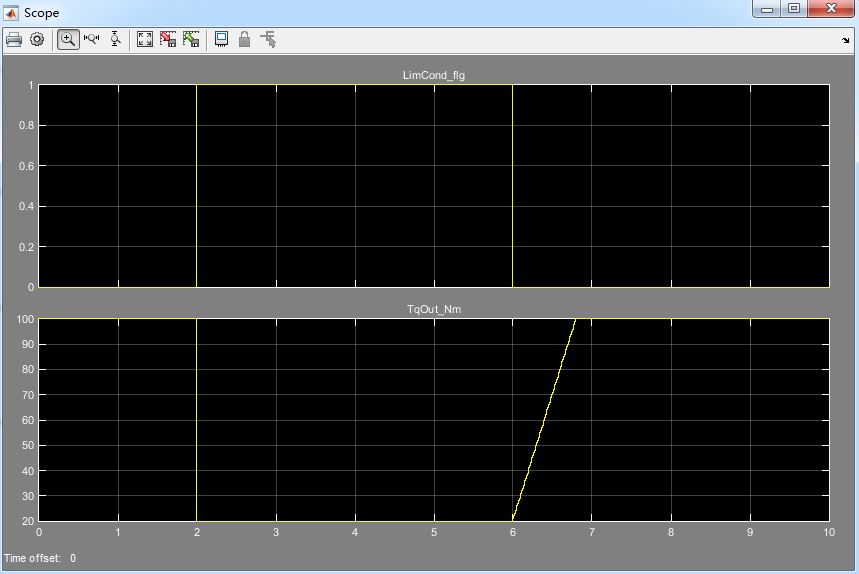
仿真结果分析如下：

1）0s~2s，TqOut_Nm为原始输入扭矩100，符合需求

2）2s，TqOut_Nm为限制最大扭矩20，符合需求

3）2s~6s，TqOut_Nm为限制最大扭矩20，符合需求

4）6s~6.8s，TqOut_Nm输出从20递增到100，递增时间0.8s（（100-20）*0.01），符合需求

5）6.8s~10s，TqOut_Nm恢复为原始输入扭矩100，符合需求

小结

以上提及的算法是作者以往的实际电控项目实施中，以整车跛行扭矩限制及恢复需求为参考，该算法已经在代码生成以及实车测试中得到充分的验证。为了方便简要介绍，模型已经经过简化处理。

之前的篇幅专门对Simulink基本库模块搭建以及仿真做了讨论，本文通过Simulink转态机State Flow的方式来进行算法的建模。经过用同样的输入激励进行模型仿真，其结果也证明了该方法仿真结果与原来方法仿真结果的一致性，从而将原来的基本模块逻辑做了优化。在确保功能不变的前提下，提高算法的可读性，同时视觉上是不是也清爽了很多呢？